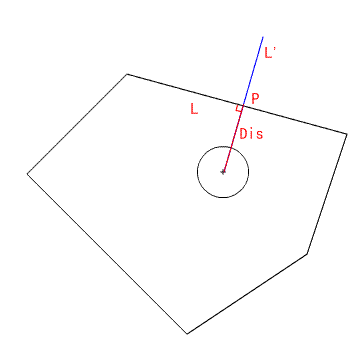
我们需要计算一下圆形的中心到直线的距离Dis,如果小于圆形的半径R,就可以知道他们已经碰撞了。
要像得到他们的距离Dis,必须知道两个点,即圆心的坐标和经过圆心的和已知直线L相垂直的直线L'的交点的坐标P。
根据直线方程y=k*x+b,我们只需要计算出k和b的值就可以确定这条经过圆心的直线L'。
因为和L垂直,我们可以计算出L'k=-(1/Lk)。根据直线L的已知两点,我们先计算出Lk=(y2-y1)/(x2-x1),x1,y1,x2,y2是已知的两点的坐标。
因此我们知道了L'k=-(x2-x1)/(y2-y1)。知道了L'k,接下来计算一下L'b,因为圆心的坐标是已知的,将其代入到y=kx+b,可以计算出L'b=y-kx;
我们最终确定了这条直线L',但是最终的目标是计算L'和L的交点,对L'和L的两个直线方程解方程组。最终我们得到了交点的坐标P。
看一下效果:(拖动圆靠近直线)
